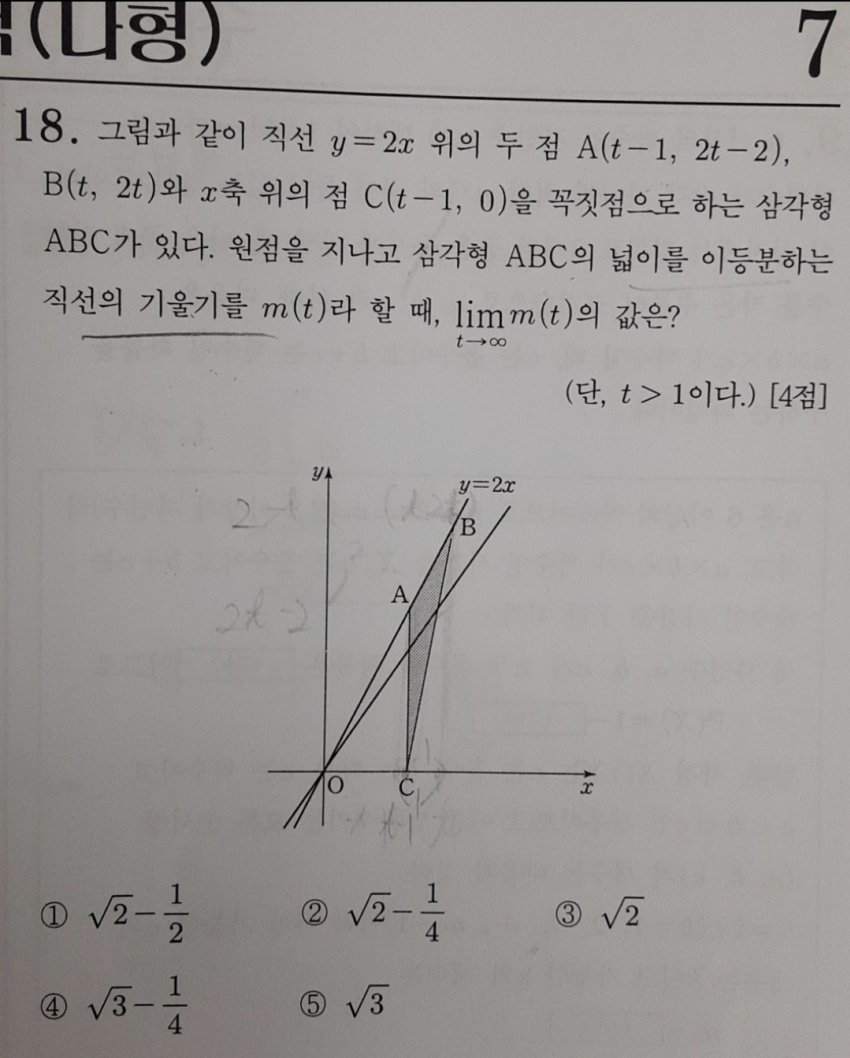
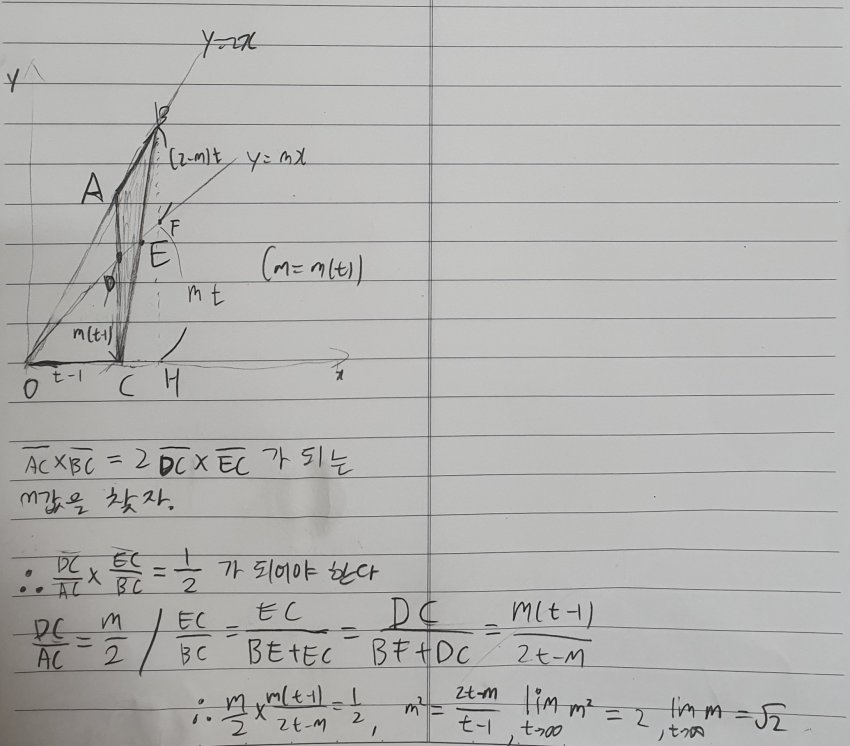이 문제를 읽어봐라 게이들은 이 문제를 어떻게 풀 생각이노? ... 모르겠노? 씹허수 ㅁㅈㅎ ㅋㅋ 대부분 이 문제를 교점의 좌표를 구하여 삼각형의 넓이를 직접 구하는 방식으로 푼다 예시:
이 문제를 읽어봐라
게이들은 이 문제를 어떻게 풀 생각이노?
...
모르겠노? 씹허수 ㅁㅈㅎ ㅋㅋ
대부분 이 문제를 교점의 좌표를 구하여
삼각형의 넓이를 직접 구하는 방식으로 푼다
예시:
(출처 : 콴다. 예쁜 글씨와 성능좋은 색펜에서 허수의 향기가 느껴진다) 그렇게 풀면 존나 귀찮다 이기야..
(출처 : 콴다. 예쁜 글씨와 성능좋은 색펜에서 허수의 향기가 느껴진다)
그렇게 풀면 존나 귀찮다 이기야..
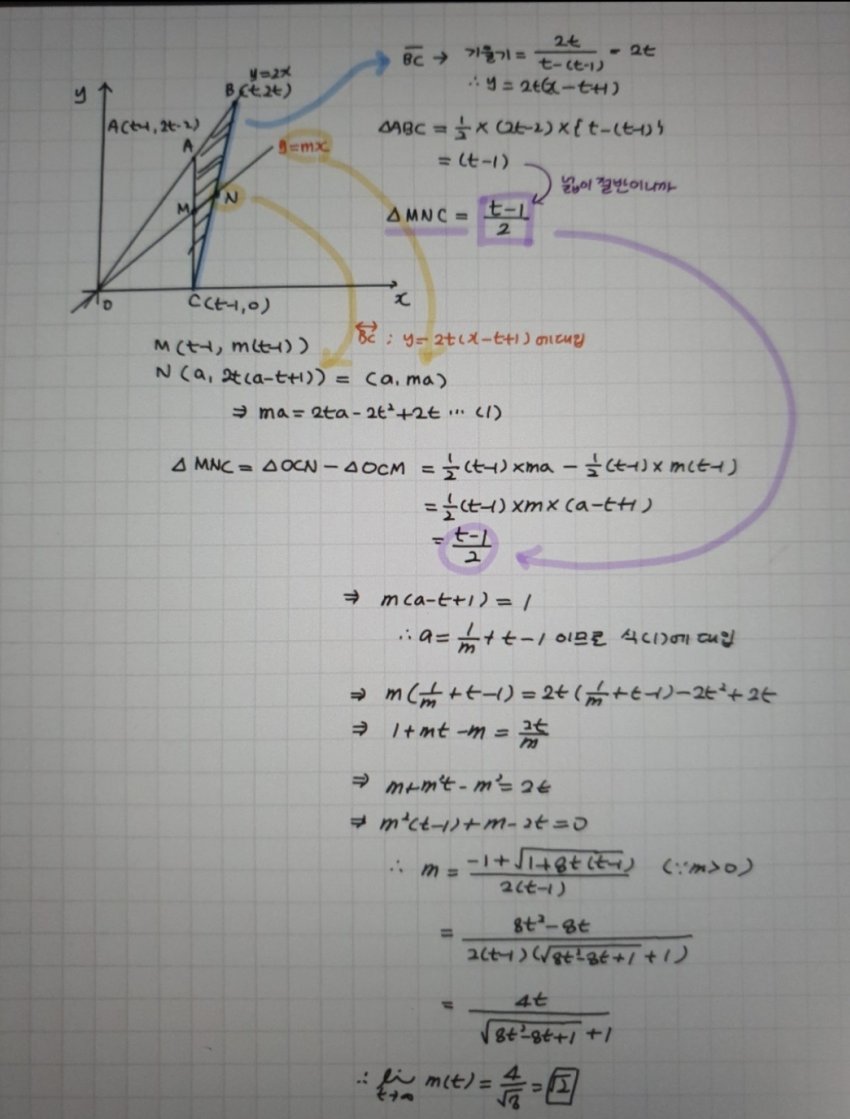
이제 내가 더 성능좋은 풀이법을 알려주겠다 삼각형의 넓이 = 2분의1 A × B × sin☆ 이 공식을 이용해서 풀어보도록 하겠노
이제 내가 더 성능좋은 풀이법을 알려주겠다
삼각형의 넓이 = 2분의1 A × B × sin☆
이 공식을 이용해서 풀어보도록 하겠노
야~기분좋다! (m² = 2t-m/t-1 에서 바로 t를 극한으로 보내 2t-m의 m을 숫자 취급 하는것도 딲좋은 SKILL이라고 할 수 있다) 역시 기하적 관점은 유용하다는 사실을 알 수 있다. 그런데 이 문제는 더욱 쉬운 풀이가 존재한다 .... ------------- t가 무한으로 가면 이 삼각형을 그냥 AC=BC이고 아주아주 뾰족한 이등변 삼각형으로 봐도 무방하다 그리고 이 삼각형이 존나게 얇아서 원점 O에서부터 팍 꽂아서 반으로 자르던 그냥 가로로 확 잘라버리던 개 좆도 차이가 안난다 그렇게 된다면 문제는 이렇게 바뀐다
야~기분좋다!
(m² = 2t-m/t-1 에서 바로 t를 극한으로 보내 2t-m의 m을 숫자 취급 하는것도 딲좋은 SKILL이라고 할 수 있다)
역시 기하적 관점은 유용하다는 사실을 알 수 있다.
그런데
이 문제는 더욱 쉬운 풀이가 존재한다 ....
-------------
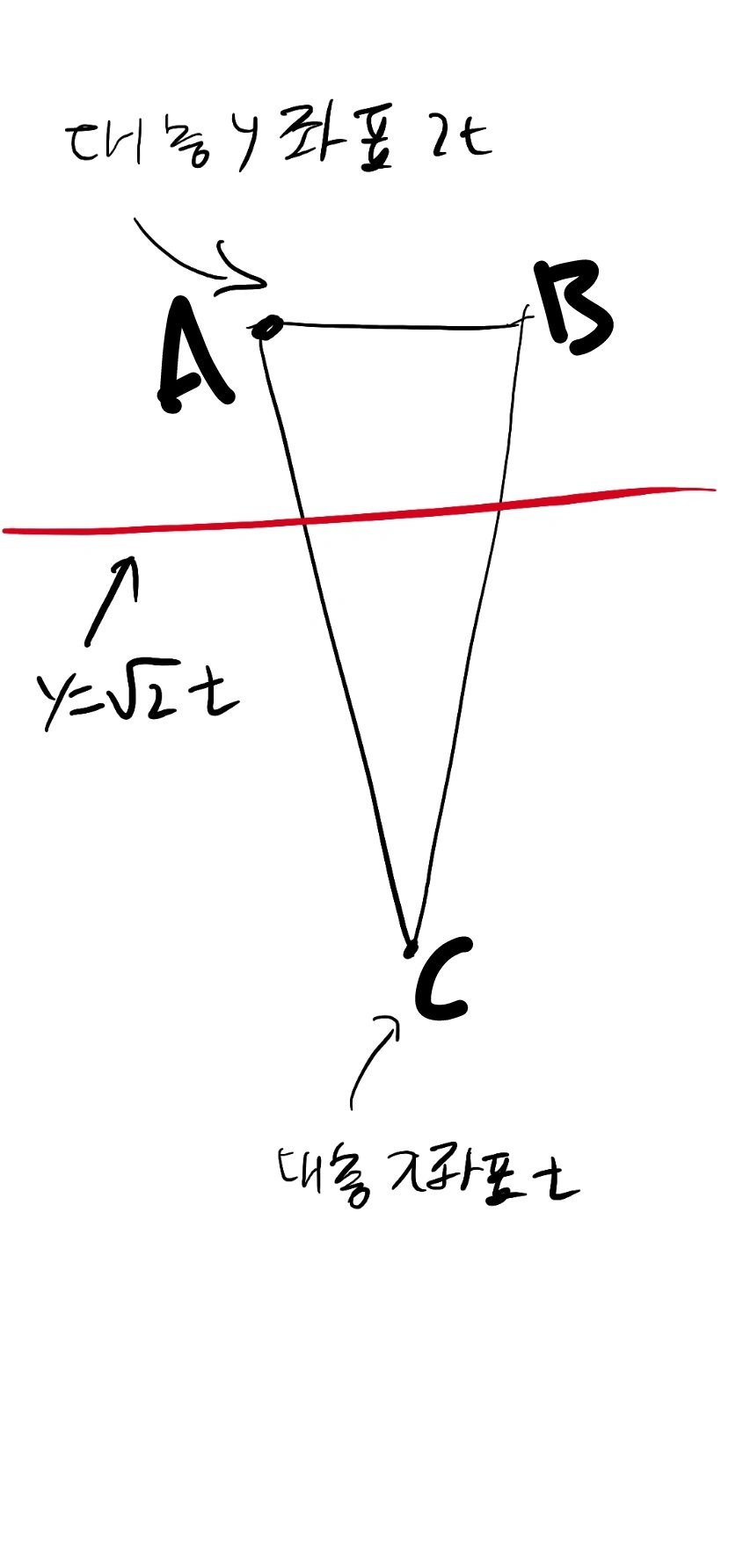
t가 무한으로 가면
이 삼각형을 그냥 AC=BC이고 아주아주 뾰족한 이등변 삼각형으로 봐도 무방하다
그리고 이 삼각형이 존나게 얇아서
원점 O에서부터 팍 꽂아서 반으로 자르던
그냥 가로로 확 잘라버리던
개 좆도 차이가 안난다
그렇게 된다면 문제는 이렇게 바뀐다
야 ~ 기분 존나 딱 좋다 따라서 m = 루트 2
야 ~ 기분 존나 딱 좋다
따라서 m = 루트 2
세번째 풀이와 같이 근사를 활용한 풀이를 잘 익히면 극한 문제는 누워서 두부먹기다 이기야~
세번째 풀이와 같이 근사를 활용한 풀이를 잘 익히면 극한 문제는 누워서 두부먹기다 이기야~