반갑다 게이들아이 문제는 현우진 뉴런 수2 띰17 4번즉 현우진을 듣는 게이라면 다 풀어봤을 문제다.게이들은 이 문제를 어떻게 풀었노?이 문제를 처음 본다면 어렵지 않으니 한번 풀어봐라
반갑다 게이들아
이 문제는 현우진 뉴런 수2 띰17 4번
즉 현우진을 듣는 게이라면 다 풀어봤을 문제다.
게이들은 이 문제를 어떻게 풀었노?
이 문제를 처음 본다면 어렵지 않으니 한번 풀어봐라
인강에서 현우진은 이 문제를 총 3가지 방법으로 해설해준다.우선 현우진의 풀이를 한번 보자
인강에서 현우진은 이 문제를 총 3가지 방법으로 해설해준다.
우선 현우진의 풀이를 한번 보자
f의 차수를 결정하는게 문제의 핵심이며 다양한 방법으로 f의 차수를 구했다.물론 아주 훌륭한 풀이고 현우진도 학생들이 딱 여기까지 체득한다면 충분하다고 생각한 듯하다 "하지만"
f의 차수를 결정하는게 문제의 핵심이며 다양한 방법으로 f의 차수를 구했다.
물론 아주 훌륭한 풀이고 현우진도 학생들이 딱 여기까지 체득한다면 충분하다고 생각한 듯하다 "하지만"
본좌는 문제를 읽자마자 f의 차수가 보여버렸다 ㅋㅋㅋㅋㅋㅋ우흥~
본좌는 문제를 읽자마자 f의 차수가 보여버렸다 ㅋㅋㅋㅋㅋㅋ우흥~
게이들아 (가) 조건을 잘 살펴보아라마치 "등차수열의 합"의 형태가 아니노?ㅋㅋㅋㅋㅋ평가원 이새끼 안 걸리려고 1 /2를 앞에다 박아놓은 꼬라지ㅋㅋㅋㅋㅋㅋㅋㅋ 딱 걸렸놐ㅋㅋㅋ
게이들아 (가) 조건을 잘 살펴보아라
마치 "등차수열의 합"의 형태가 아니노?ㅋㅋㅋㅋㅋ
평가원 이새끼 안 걸리려고 1 /2를 앞에다 박아놓은 꼬라지ㅋㅋㅋㅋㅋㅋㅋㅋ 딱 걸렸놐ㅋㅋㅋ
등차수열의 합 공식은 "평균x항의 개수"이다(가) 조건을 (x-1){f(x) + f(1)}/2로 본다면 딱 그 형태가 아니노? ㅋㅋㅋㅋㅋㅋ 정적분의 성질이 시그마와 매우 유사함을 고려했을때 항의개수=정적분의 구간 즉 "사이즈"를 의미한다.(가)조건에서 1부터 x까지 적분하고자 했으니 사이즈는 x-1이 되는것이지 ㅋㅋㅋㅋㅋㅋㅋㅋ
등차수열의 합 공식은 "평균x항의 개수"이다
(가) 조건을 (x-1){f(x) + f(1)}/2로 본다면 딱 그 형태가 아니노? ㅋㅋㅋㅋㅋㅋ
정적분의 성질이 시그마와 매우 유사함을 고려했을때 항의개수=정적분의 구간 즉 "사이즈"를 의미한다.
(가)조건에서 1부터 x까지 적분하고자 했으니 사이즈는 x-1이 되는것이지 ㅋㅋㅋㅋㅋㅋㅋㅋ
따라서 f의 정적분값=등차수열의 합이니f는 1차식이다 ㅋㅋㅋㅋㅋㅋ(이해가 안간다면 살짝미분/적분과 비슷한 개념으로 생각해봐라)
따라서 f의 정적분값=등차수열의 합이니
f는 1차식이다 ㅋㅋㅋㅋㅋㅋ
(이해가 안간다면 살짝미분/적분과 비슷한 개념으로 생각해봐라)
시그마와 적분의 개념이 비슷하다는 점를 이용하여 생각해보는 나름 좋은 접근이라고 생각한다.이후 풀이는 현우진과 동일하니생략한다더 좋은 풀이가 있다면 댓글로 알려주고 유익했다면 개추 부탁하노
시그마와 적분의 개념이 비슷하다는 점를 이용하여 생각해보는 나름 좋은 접근이라고 생각한다.
이후 풀이는 현우진과 동일하니
생략한다
더 좋은 풀이가 있다면 댓글로 알려주고 유익했다면 개추 부탁하노



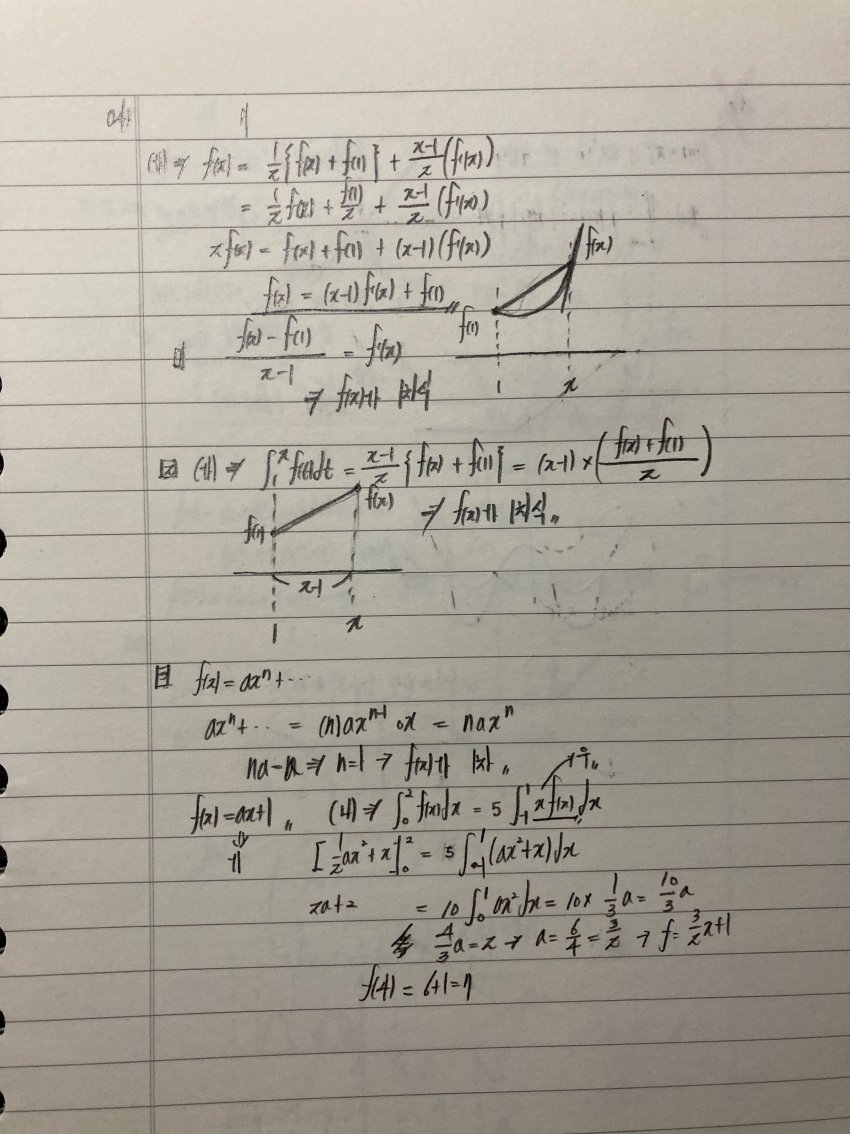





 ㅈ반고 수붕이.. 실시간 온라인 체육대회중 이새끼 뭐냐?
ㅈ반고 수붕이.. 실시간 온라인 체육대회중 이새끼 뭐냐?
 수붕이... 실시간 개ㅈ됐다...jpg
수붕이... 실시간 개ㅈ됐다...jpg















