22번 문제 풀이 세타가 30도 일때 CEF는 1 : 루트3 : 2 특수각 삼각형 CB = EB = 1 그리고 각 CBE는 3세타 - 90도 세타 - 30도 를 알파라고 하면 각 CBE는 3알파 세타가 30도 일때 알파는 0이고 CB = EB = 1 이므로 CE는 3알파 이고 삼각형 CEF는 알파² × 3루트3 / 2 따라서 구하는 값은 3루트3 / 2
22번 문제 풀이
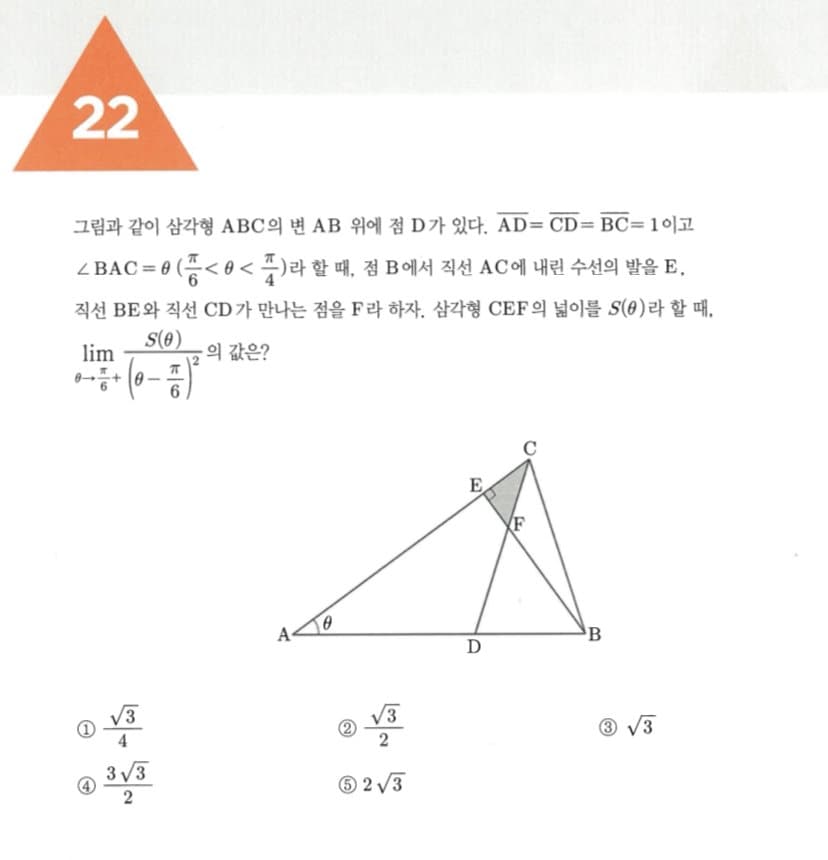
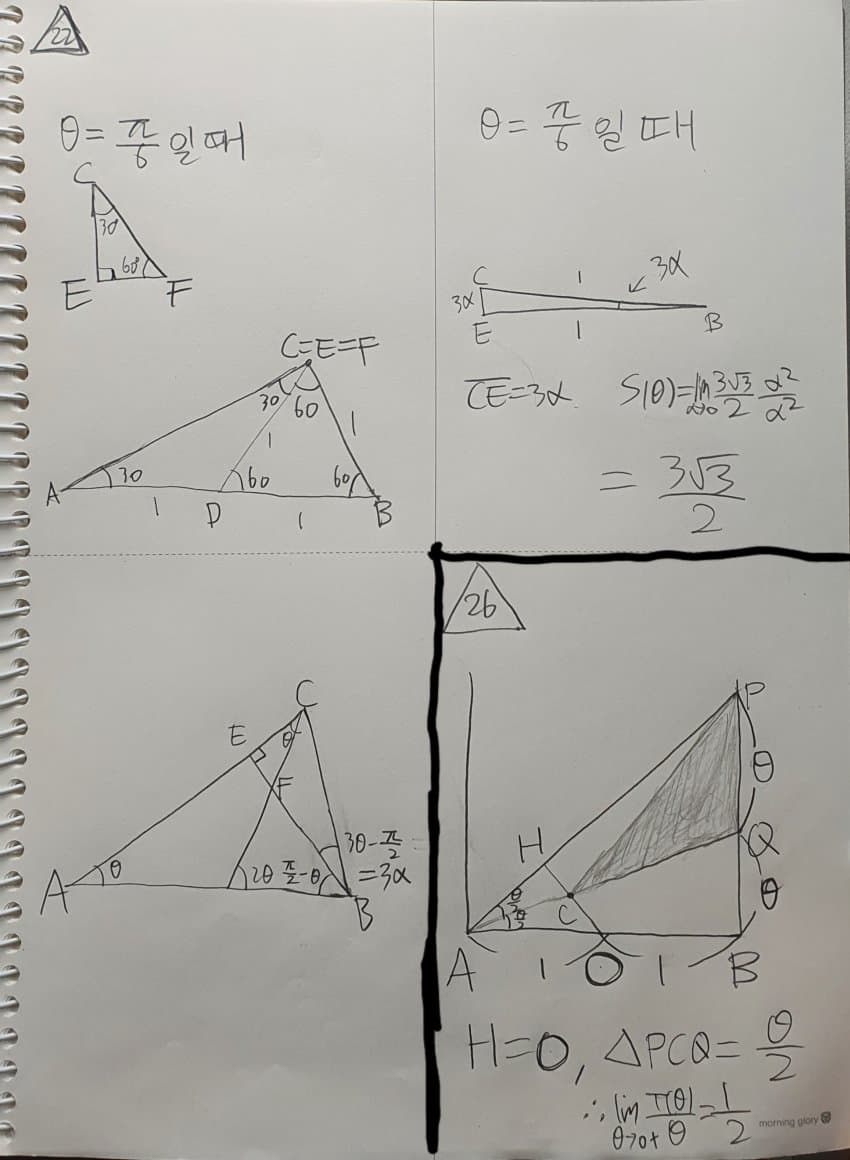
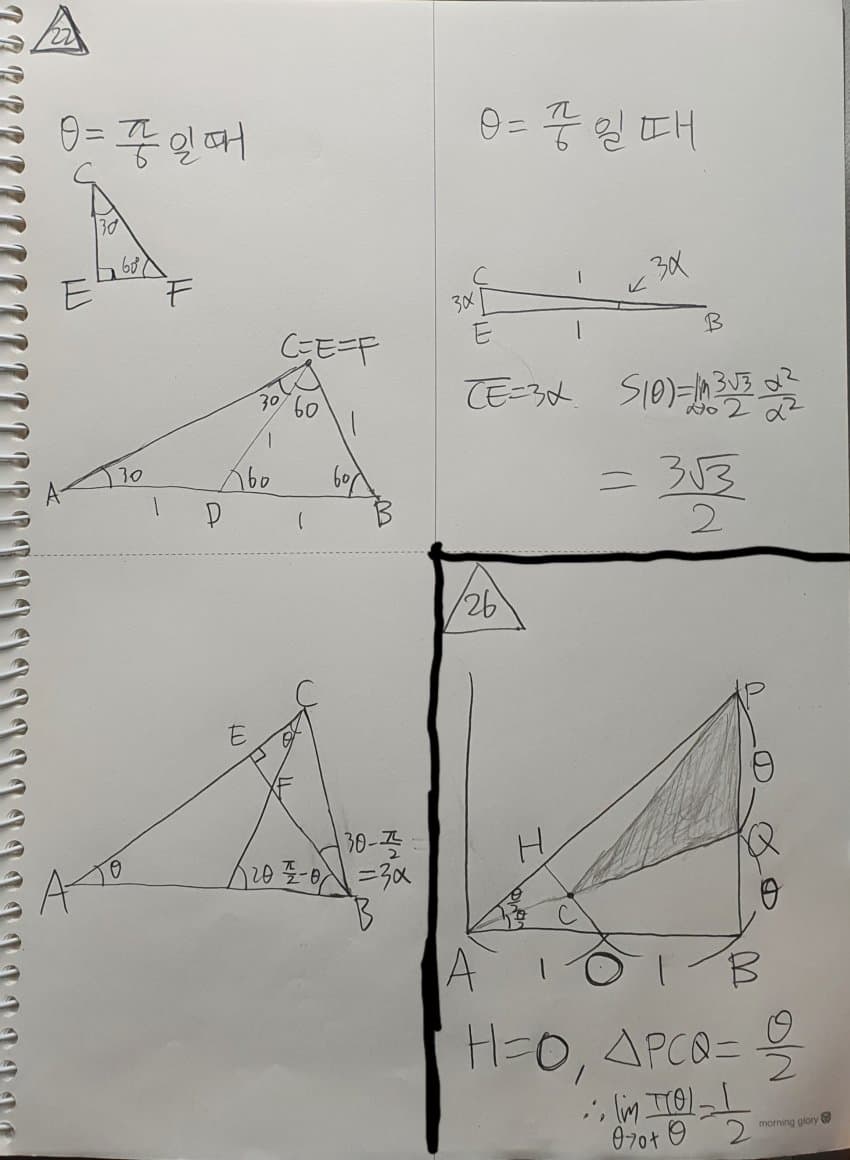
세타가 30도 일때 CEF는 1 : 루트3 : 2 특수각 삼각형
CB = EB = 1
그리고 각 CBE는 3세타 - 90도
세타 - 30도 를 알파라고 하면 각 CBE는 3알파
세타가 30도 일때 알파는 0이고 CB = EB = 1 이므로
CE는 3알파 이고
삼각형 CEF는
알파² × 3루트3 / 2
따라서 구하는 값은 3루트3 / 2
26번 문제 풀이 세타가 0으로 가기 때문에 반원을 두 개의 직각을 가진 도형으로 근사해도 무방하다 AB = 2이고 각 QAB와 각 PAQ가 세타 / 2 이다 따라서 PQ = QB = 세타 세타가 0으로 갈 때 H = C = O 이다 그러므로 삼각형 PCQ의 넓이는 세타 / 2 따라서 구하는 값은 1/2
26번 문제 풀이
세타가 0으로 가기 때문에
반원을 두 개의 직각을 가진 도형으로 근사해도 무방하다
AB = 2이고 각 QAB와 각 PAQ가 세타 / 2 이다 따라서
PQ = QB = 세타
세타가 0으로 갈 때 H = C = O 이다 그러므로
삼각형 PCQ의 넓이는 세타 / 2
따라서 구하는 값은 1/2