Math IDEA & SKILL - 1 (6모 21번)
반갑다 게이들아이 문제는 6모를 본 게이들이라면 풀어봤을 공통 21번 문제다게이들은 이 문제를 어떻게 풀었노?잠시 생각해봐라..
반갑다 게이들아
이 문제는 6모를 본 게이들이라면 풀어봤을 공통 21번 문제다
게이들은 이 문제를 어떻게 풀었노?
잠시 생각해봐라..
아마 대부분이 f(x)를 (x-a)(x-b)로 잡고 n에 1부터 벅벅 집어 넣어봤을거다 ㅋㅋ
아마 대부분이 f(x)를 (x-a)(x-b)로 잡고
n에 1부터 벅벅 집어 넣어봤을거다 ㅋㅋ
물론 이런 출발도 매우 good~우흥현우진을 들은 게이들이라면 알테지만 모르면 대입하는 건 좋은 자세다 이기야
물론 이런 출발도 매우 good~우흥
현우진을 들은 게이들이라면 알테지만 모르면 대입하는 건 좋은 자세다 이기야
하지만 이렇게 해버리면 n에 대입하는 수가 커질수록 풀이과정이 역겹다 수붕이들을 위해 성능좋은 풀이 한가지 알려주겠노 ㅋㅋㅋㅋㅋㅋㅋ예아~
하지만 이렇게 해버리면 n에 대입하는 수가 커질수록 풀이과정이 역겹다
수붕이들을 위해 성능좋은 풀이 한가지 알려주겠노 ㅋㅋㅋㅋㅋㅋㅋ예아~
n에 1부터 숫자를 대입해본 게이들이라면 바로 눈치를 챘을거다 n이 홀수일때는 (가)조건에 위배되기 때문에 n이 짝수라는 사실쯤은 눈치챘겠지? 우흥~ㅋㅋㅋㅋㅋㅋ
n에 1부터 숫자를 대입해본 게이들이라면 바로 눈치를 챘을거다
n이 홀수일때는 (가)조건에 위배되기 때문에 n이 짝수라는 사실쯤은 눈치챘겠지? 우흥~ㅋㅋㅋㅋㅋㅋ
그렇다면 게이들아 잘생각해봐라..n이 짝수라면 방정식의 해의 절댓값은 같지 않노?? 따라서 f(x)를 (x-a)(x+a)로 잡는게 이 문제의 핵심이다
그렇다면 게이들아 잘생각해봐라..
n이 짝수라면 방정식의 해의 절댓값은 같지 않노??
따라서 f(x)를 (x-a)(x+a)로 잡는게 이 문제의 핵심이다
그렇다면 (나)조건에 해당하는 f의 최솟값은 a^2이고 a^2이 정수임을 만족시키는 짝수 n을 전부 찾아버리면 게임 끝ㅋㅋㅋㅋㅋㅋㅋ딱 좋노~~ㅋㅋㅋ(가)의 조건에 따라 a^n=64이므로n에 2부터 짝수를 하나씩 대입해보자
그렇다면 (나)조건에 해당하는 f의 최솟값은 a^2이고 a^2이 정수임을 만족시키는 짝수 n을 전부 찾아버리면 게임 끝ㅋㅋㅋㅋㅋㅋㅋ딱 좋노~~ㅋㅋㅋ
(가)의 조건에 따라 a^n=64이므로
n에 2부터 짝수를 하나씩 대입해보자
n=2, 4, 6, 12일때 성립하고8,10일때는 성립하지 않는다 왜냐면 a^2이 정수가 아니기 때문..
n=2, 4, 6, 12일때 성립하고
8,10일때는 성립하지 않는다 왜냐면 a^2이 정수가 아니기 때문..
따라서 답은 24다 게이들아 ㅋㅋ유익했으면 개추 부탁하고또다른 성능좋은 풀이를 발견했다면 댓글로 공유 부탁하노ㅋㅋㅋㅋㅋ
따라서 답은 24다 게이들아 ㅋㅋ
유익했으면 개추 부탁하고
또다른 성능좋은 풀이를 발견했다면 댓글로 공유 부탁하노ㅋㅋㅋㅋㅋ








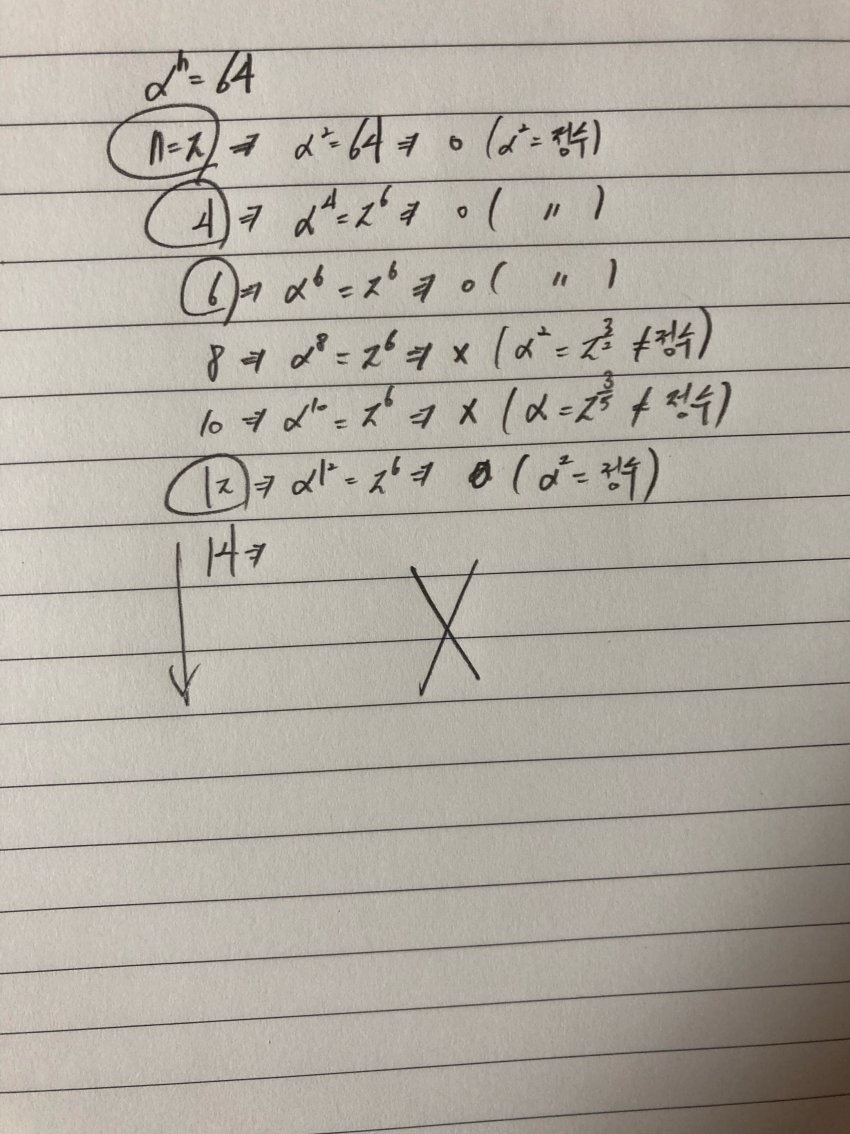

 공통 수학 도형 문제 암산 풀이 ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ
공통 수학 도형 문제 암산 풀이 ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ